mirror of
https://github.com/trekhleb/javascript-algorithms.git
synced 2025-04-07 06:41:07 +08:00
Brazilian Portuguese translation and typos fixes (#943)
* Update README.pt-BR.md * TRIE README.pt-BR typo * TREE README.pt-BR typo * Stack README.pt-BR typo * Priority Queue README.pt-BR typo * hash-table README.pt-BR typo * doubly-linked-list README.pt-BR typo * disjoint-set README.pt-BR typo * bloom-filter README.pt-BR typo * merge-sort pt-BR translation * merge-sort README added pt-BR option * insertion sort pt-BR translation * insertion sort README added pt-br option * heap-sort pt-BR translation * heap-sort READMED added pt-BR option * bubble sort pt-BR typo * pt-BR translation for sorting algorithms Fixed typos and translated all the missing algorithms * Update README.pt-BR.md * linked list pt-BR translation * ml pt-BR translation * fix typo in README Co-authored-by: Oleksii Trekhleb <trehleb@gmail.com>
This commit is contained in:
parent
9ef6650207
commit
da6ae08851
217
README.pt-BR.md
217
README.pt-BR.md
@ -31,9 +31,7 @@ _Leia isto em outros idiomas:_
|
||||
## Estrutura de Dados
|
||||
|
||||
Uma estrutura de dados é uma maneira particular de organizar e armazenar dados em um computador para que ele possa
|
||||
ser acessado e modificado de forma eficiente. Mais precisamente, uma estrutura de dados é uma coleção de dados
|
||||
valores, as relações entre eles e as funções ou operações que podem ser aplicadas a
|
||||
os dados.
|
||||
ser acessado e modificado de forma eficiente. Mais precisamente, uma estrutura de dados é uma coleção de valores de dados, as relações entre eles e as funções ou operações que podem ser aplicadas aos dados.
|
||||
|
||||
`B` - Iniciante, `A` - Avançado
|
||||
|
||||
@ -42,17 +40,17 @@ os dados.
|
||||
* `B` [Fila (Queue)](src/data-structures/queue/README.pt-BR.md)
|
||||
* `B` [Pilha (Stack)](src/data-structures/stack/README.pt-BR.md)
|
||||
* `B` [Tabela de Hash (Hash Table)](src/data-structures/hash-table/README.pt-BR.md)
|
||||
* `B` [Heap](src/data-structures/heap/README.pt-BR.md)
|
||||
* `B` [Heap](src/data-structures/heap/README.pt-BR.md) - versões de heap máximo e mínimo
|
||||
* `B` [Fila de Prioridade (Priority Queue)](src/data-structures/priority-queue/README.pt-BR.md)
|
||||
* `A` [Árvore de prefixos (Trie)](src/data-structures/trie/README.pt-BR.md)
|
||||
* `A` [Árvore de Prefixos (Trie)](src/data-structures/trie/README.pt-BR.md)
|
||||
* `A` [Árvore (Tree)](src/data-structures/tree/README.pt-BR.md)
|
||||
* `A` [Árvore de Pesquisa Binária (Binary Search Tree)](src/data-structures/tree/binary-search-tree/README.pt-BR.md)
|
||||
* `A` [Árvore AVL (AVL Tree)](src/data-structures/tree/avl-tree/README.pt-BR.md)
|
||||
* `A` [Árvore Vermelha-Preta (Red-Black Tree)](src/data-structures/tree/red-black-tree/README.pt-BR.md)
|
||||
* `A` [Árvore de Segmento (Segment Tree)](src/data-structures/tree/segment-tree/README.pt-BR.md) - Com exemplos de consultas min / max / sum range
|
||||
* `A` [Árvore Rubro-Negra (Red-Black Tree)](src/data-structures/tree/red-black-tree/README.pt-BR.md)
|
||||
* `A` [Árvore de Segmento (Segment Tree)](src/data-structures/tree/segment-tree/README.pt-BR.md) - com exemplos de consultas min / max / sum range
|
||||
* `A` [Árvore Fenwick (Fenwick Tree)](src/data-structures/tree/fenwick-tree/README.pt-BR.md) (Árvore indexada binária)
|
||||
* `A` [Grafo (Graph)](src/data-structures/graph/README.pt-BR.md) (ambos dirigidos e não direcionados)
|
||||
* `A` [Conjunto Disjuntor (Disjoint Set)](src/data-structures/disjoint-set/README.pt-BR.md)
|
||||
* `A` [Conjunto Disjunto (Disjoint Set)](src/data-structures/disjoint-set/README.pt-BR.md)
|
||||
* `A` [Filtro Bloom (Bloom Filter)](src/data-structures/bloom-filter/README.pt-BR.md)
|
||||
|
||||
## Algoritmos
|
||||
@ -72,36 +70,37 @@ um conjunto de regras que define precisamente uma sequência de operações.
|
||||
* `B` [Algoritmo Euclidiano](src/algorithms/math/euclidean-algorithm) - Calcular o Máximo Divisor Comum (MDC)
|
||||
* `B` [Mínimo Múltiplo Comum](src/algorithms/math/least-common-multiple) Calcular o Mínimo Múltiplo Comum (MMC)
|
||||
* `B` [Peneira de Eratóstenes](src/algorithms/math/sieve-of-eratosthenes) - Encontrar todos os números primos até um determinado limite
|
||||
* `B` [Potência de dois](src/algorithms/math/is-power-of-two) - Verifique se o número é a potência de dois (algoritmos ingênuos e bit a bit)
|
||||
* `B` [Potência de Dois](src/algorithms/math/is-power-of-two) - Verifique se o número é a potência de dois (algoritmos ingênuos e bit a bit)
|
||||
* `B` [Triângulo de Pascal](src/algorithms/math/pascal-triangle)
|
||||
* `B` [Número complexo](src/algorithms/math/complex-number) - Números complexos e operações básicas com eles
|
||||
* `A` [Partição inteira](src/algorithms/math/integer-partition)
|
||||
* `B` [Número Complexo](src/algorithms/math/complex-number) - Números complexos e operações básicas com eles
|
||||
* `A` [Partição Inteira](src/algorithms/math/integer-partition)
|
||||
* `A` [Algoritmo Liu Hui π](src/algorithms/math/liu-hui) - Cálculos aproximados de π baseados em N-gons
|
||||
* **Conjuntos**
|
||||
* `B` [Produto cartesiano](src/algorithms/sets/cartesian-product) - Produto de vários conjuntos
|
||||
* `B` [Produto Cartesiano](src/algorithms/sets/cartesian-product) - Produto de vários conjuntos
|
||||
* `B` [Permutações de Fisher–Yates](src/algorithms/sets/fisher-yates) - Permutação aleatória de uma sequência finita
|
||||
* `A` [Potência e Conjunto](src/algorithms/sets/power-set) - Todos os subconjuntos de um conjunto
|
||||
* `A` [Permutações](src/algorithms/sets/permutations) (com e sem repetições)
|
||||
* `A` [Combinações](src/algorithms/sets/combinations) (com e sem repetições)
|
||||
* `A` [Mais longa subsequência comum](src/algorithms/sets/longest-common-subsequence) (LCS)
|
||||
* `A` [Maior subsequência crescente](src/algorithms/sets/longest-increasing-subsequence)
|
||||
* `A` [Supersequência Comum mais curta](src/algorithms/sets/shortest-common-supersequence) (SCS)
|
||||
* `A` [Problema da mochila](src/algorithms/sets/knapsack-problem) - "0/1" e "Não consolidado"
|
||||
* `A` [Máximo Subarray](src/algorithms/sets/maximum-subarray) - "Força bruta" e " Programação Dinâmica" versões (Kadane's)
|
||||
* `A` [Mais Longa Subsequência Comum](src/algorithms/sets/longest-common-subsequence) (LCS)
|
||||
* `A` [Maior Subsequência Crescente](src/algorithms/sets/longest-increasing-subsequence)
|
||||
* `A` [Supersequência Comum Mais Curta](src/algorithms/sets/shortest-common-supersequence) (SCS)
|
||||
* `A` [Problema da Mochila](src/algorithms/sets/knapsack-problem) - "0/1" e "Não consolidado"
|
||||
* `A` [Subarray Máximo](src/algorithms/sets/maximum-subarray) - "Força bruta" e "Programação Dinâmica", versões de Kadane
|
||||
* `A` [Soma de Combinação](src/algorithms/sets/combination-sum) - Encontre todas as combinações que formam uma soma específica
|
||||
* **Cadeia de Caracteres**
|
||||
* `B` [Hamming Distance](src/algorithms/string/hamming-distance) - Número de posições em que os símbolos são diferentes
|
||||
* `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - Distância mínima de edição entre duas sequências
|
||||
* `A` [Knuth–Morris–Pratt Algorithm](src/algorithms/string/knuth-morris-pratt) (Algoritmo KMP) - Pesquisa de substring (correspondência de padrão)
|
||||
* `B` [Distância de Hamming](src/algorithms/string/hamming-distance) - Número de posições em que os símbolos são diferentes
|
||||
* `B` [Palíndromos](src/algorithms/string/palindrome) - Verifique se a cadeia de caracteres (string) é a mesma ao contrário
|
||||
* `A` [Distância Levenshtein](src/algorithms/string/levenshtein-distance) - Distância mínima de edição entre duas sequências
|
||||
* `A` [Algoritmo Knuth–Morris–Pratt](src/algorithms/string/knuth-morris-pratt) (Algoritmo KMP) - Pesquisa de substring (correspondência de padrão)
|
||||
* `A` [Z Algorithm](src/algorithms/string/z-algorithm) - Pesquisa de substring (correspondência de padrão)
|
||||
* `A` [Rabin Karp Algorithm](src/algorithms/string/rabin-karp) - Pesquisa de substring
|
||||
* `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
|
||||
* `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
|
||||
* `A` [Algoritmo de Rabin Karp](src/algorithms/string/rabin-karp) - Pesquisa de substring
|
||||
* `A` [Substring Comum Mais Longa](src/algorithms/string/longest-common-substring)
|
||||
* `A` [Expressões Regulares Correspondentes](src/algorithms/string/regular-expression-matching)
|
||||
* **Buscas**
|
||||
* `B` [Linear Search](src/algorithms/search/linear-search)
|
||||
* `B` [Jump Search](src/algorithms/search/jump-search) (ou Bloquear pesquisa) - Pesquisar na matriz ordenada
|
||||
* `B` [Binary Search](src/algorithms/search/binary-search) - Pesquisar na matriz ordenada
|
||||
* `B` [Interpolation Search](src/algorithms/search/interpolation-search) - Pesquisar em matriz classificada uniformemente distribuída
|
||||
* `B` [Busca Linear (Linear Search)](src/algorithms/search/linear-search)
|
||||
* `B` [Busca por Saltos (Jump Search)](src/algorithms/search/jump-search) - Pesquisa em matriz ordenada
|
||||
* `B` [Busca Binária (Binary Search)](src/algorithms/search/binary-search) - Pesquisa em matriz ordenada
|
||||
* `B` [Busca por Interpolação (Interpolation Search)](src/algorithms/search/interpolation-search) - Pesquisa em matriz classificada uniformemente distribuída
|
||||
* **Classificação**
|
||||
* `B` [Bubble Sort](src/algorithms/sorting/bubble-sort)
|
||||
* `B` [Selection Sort](src/algorithms/sorting/selection-sort)
|
||||
@ -112,35 +111,35 @@ um conjunto de regras que define precisamente uma sequência de operações.
|
||||
* `B` [Shellsort](src/algorithms/sorting/shell-sort)
|
||||
* `B` [Counting Sort](src/algorithms/sorting/counting-sort)
|
||||
* `B` [Radix Sort](src/algorithms/sorting/radix-sort)
|
||||
* **Arvóres**
|
||||
* `B` [Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
|
||||
* `B` [Breadth-First Search](src/algorithms/tree/breadth-first-search) (BFS)
|
||||
* **Árvores**
|
||||
* `B` [Busca em Profundidade (Depth-First Search)](src/algorithms/tree/depth-first-search) (DFS)
|
||||
* `B` [Busca em Largura (Breadth-First Search)](src/algorithms/tree/breadth-first-search) (BFS)
|
||||
* **Grafos**
|
||||
* `B` [Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
|
||||
* `B` [Breadth-First Search](src/algorithms/graph/breadth-first-search) (BFS)
|
||||
* `B` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - Encontrar Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
|
||||
* `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - Encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
|
||||
* `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - Encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
|
||||
* `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - Encontrar caminhos mais curtos entre todos os pares de vértices
|
||||
* `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - Para gráficos direcionados e não direcionados (versões baseadas em DFS e Conjunto Disjuntivo)
|
||||
* `A` [Prim’s Algorithm](src/algorithms/graph/prim) - Encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
|
||||
* `A` [Topological Sorting](src/algorithms/graph/topological-sorting) - Métodos DFS
|
||||
* `A` [Articulation Points](src/algorithms/graph/articulation-points) -O algoritmo de Tarjan (baseado em DFS)
|
||||
* `A` [Bridges](src/algorithms/graph/bridges) - Algoritmo baseado em DFS
|
||||
* `A` [Eulerian Path and Eulerian Circuit](src/algorithms/graph/eulerian-path) - Algoritmo de Fleury - Visite todas as bordas exatamente uma vez
|
||||
* `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visite todas as bordas exatamente uma vez
|
||||
* `A` [Strongly Connected Components](src/algorithms/graph/strongly-connected-components) - Algoritmo de Kosaraju's
|
||||
* `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - Rota mais curta possível que visita cada cidade e retorna à cidade de origem
|
||||
* `B` [Busca em Profundidade (Depth-First Search)](src/algorithms/graph/depth-first-search) (DFS)
|
||||
* `B` [Busca em Largura (Breadth-First Search)](src/algorithms/graph/breadth-first-search) (BFS)
|
||||
* `B` [Algoritmo de Kruskal](src/algorithms/graph/kruskal) - Encontrando Árvore Mínima de Abrangência (MST) para grafo conexo com pesos
|
||||
* `A` [Algoritmo de Dijkstra](src/algorithms/graph/dijkstra) - Encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
|
||||
* `A` [Algoritmo de Bellman-Ford](src/algorithms/graph/bellman-ford) - Encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
|
||||
* `A` [Algoritmo de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - Encontrar caminhos mais curtos entre todos os pares de vértices
|
||||
* `A` [Detectar Ciclo](src/algorithms/graph/detect-cycle) - Para grafos direcionados e não direcionados (versões baseadas em DFS e Conjunto Disjuntivo)
|
||||
* `A` [Algoritmo de Prim](src/algorithms/graph/prim) - Encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
|
||||
* `A` [Ordenação Topológica](src/algorithms/graph/topological-sorting) - Métodos DFS
|
||||
* `A` [Pontos de Articulação](src/algorithms/graph/articulation-points) - O algoritmo de Tarjan (baseado em DFS)
|
||||
* `A` [Pontes](src/algorithms/graph/bridges) - Algoritmo baseado em DFS
|
||||
* `A` [Caminho e Circuito Euleriano](src/algorithms/graph/eulerian-path) - Algoritmo de Fleury - Visite todas as bordas exatamente uma vez
|
||||
* `A` [Ciclo Hamiltoniano](src/algorithms/graph/hamiltonian-cycle) - Visite todas as bordas exatamente uma vez
|
||||
* `A` [Componentes Fortemente Conectados](src/algorithms/graph/strongly-connected-components) - Algoritmo de Kosaraju
|
||||
* `A` [Problema do Caixeiro Viajante](src/algorithms/graph/travelling-salesman) - Rota mais curta possível que visita cada cidade e retorna à cidade de origem
|
||||
* **Criptografia**
|
||||
* `B` [Polynomial Hash](src/algorithms/cryptography/polynomial-hash) - Função de hash de rolagem baseada em polinômio
|
||||
* `B` [Hash Polinomial](src/algorithms/cryptography/polynomial-hash) - Função de hash de rolagem baseada em polinômio
|
||||
* **Sem categoria**
|
||||
* `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
|
||||
* `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - Algoritmo no local
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game) - Backtracking, programação dinâmica (top-down + bottom-up) e exemplos gananciosos
|
||||
* `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - Backtracking, programação dinâmica e exemplos baseados no triângulo de Pascal
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - Trapping problema da água da chuva (programação dinâmica e versões de força bruta)
|
||||
* `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
|
||||
* `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
|
||||
* `B` [Torre de Hanoi](src/algorithms/uncategorized/hanoi-tower)
|
||||
* `B` [Rotação de Matriz Quadrada](src/algorithms/uncategorized/square-matrix-rotation) - Algoritmo no local
|
||||
* `B` [Jogo do Salto](src/algorithms/uncategorized/jump-game) - Backtracking, programação dinâmica (top-down + bottom-up) e exemplos gananciosos
|
||||
* `B` [Caminhos Únicos](src/algorithms/uncategorized/unique-paths) - Backtracking, programação dinâmica e exemplos baseados no triângulo de Pascal
|
||||
* `B` [Terraços de Chuva](src/algorithms/uncategorized/rain-terraces) - Problema de retenção da água da chuva (programação dinâmica e versões de força bruta)
|
||||
* `A` [Problema das N-Rainhas](src/algorithms/uncategorized/n-queens)
|
||||
* `A` [Passeio do Cavaleiro](src/algorithms/uncategorized/knight-tour)
|
||||
|
||||
### Algoritmos por Paradigma
|
||||
|
||||
@ -149,54 +148,52 @@ de algoritmos. É uma abstração maior do que a noção de um algoritmo, assim
|
||||
algoritmo é uma abstração maior que um programa de computador.
|
||||
|
||||
* **Força bruta** - Pense em todas as possibilidades e escolha a melhor solução
|
||||
* `B` [Linear Search](src/algorithms/search/linear-search)
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - Trapping problema da água da chuva
|
||||
* `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
|
||||
* `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - Rota mais curta possível que visita cada cidade e retorna à cidade de origem
|
||||
* `B` [Busca Linear (Linear Search)](src/algorithms/search/linear-search)
|
||||
* `B` [Terraços de Chuva](src/algorithms/uncategorized/rain-terraces) - Problema de retenção de água da chuva (programação dinâmica e versões de força bruta)
|
||||
* `A` [Subarray Máximo](src/algorithms/sets/maximum-subarray)
|
||||
* `A` [Problema do Caixeiro Viajante](src/algorithms/graph/travelling-salesman) - Rota mais curta possível que visita cada cidade e retorna à cidade de origem
|
||||
* **Ganância** - Escolha a melhor opção no momento, sem qualquer consideração pelo futuro
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game)
|
||||
* `A` [Unbound Knapsack Problem](src/algorithms/sets/knapsack-problem)
|
||||
* `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - Encontrar o caminho mais curto para todos os vértices do gráfico
|
||||
* `A` [Prim’s Algorithm](src/algorithms/graph/prim) - Encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
|
||||
* `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - Encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
|
||||
* `B` [Jogo do Salto](src/algorithms/uncategorized/jump-game)
|
||||
* `A` [Problema da Mochila](src/algorithms/sets/knapsack-problem)
|
||||
* `A` [Algoritmo de Dijkstra](src/algorithms/graph/dijkstra) - Encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
|
||||
* `A` [Algoritmo de Prim](src/algorithms/graph/prim) - Encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
|
||||
* `A` [Algoritmo de Kruskal](src/algorithms/graph/kruskal) - Encontrando Árvore Mínima de Abrangência (MST) para grafo conexo com pesos
|
||||
* **Dividir e Conquistar** - Dividir o problema em partes menores e então resolver essas partes
|
||||
* `B` [Busca binária (Binary Search)](src/algorithms/search/binary-search)
|
||||
* `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
|
||||
* `B` [Pascal's Triangle](src/algorithms/math/pascal-triangle)
|
||||
* `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - Calcular o Máximo Divisor Comum (MDC)
|
||||
* `B` [Busca Binária (Binary Search)](src/algorithms/search/binary-search)
|
||||
* `B` [Torre de Hanoi](src/algorithms/uncategorized/hanoi-tower)
|
||||
* `B` [Triângulo de Pascal](src/algorithms/math/pascal-triangle)
|
||||
* `B` [Algoritmo Euclidiano](src/algorithms/math/euclidean-algorithm) - Calcular o Máximo Divisor Comum (MDC)
|
||||
* `B` [Merge Sort](src/algorithms/sorting/merge-sort)
|
||||
* `B` [Quicksort](src/algorithms/sorting/quick-sort)
|
||||
* `B` [Tree Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
|
||||
* `B` [Graph Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game)
|
||||
* `A` [Permutations](src/algorithms/sets/permutations) (com e sem repetições)
|
||||
* `A` [Combinations](src/algorithms/sets/combinations) (com e sem repetições)
|
||||
* `B` [Busca em Profundidade (Depth-First Search)](src/algorithms/tree/depth-first-search) (DFS)
|
||||
* `B` [Busca em Largura (Breadth-First Search)](src/algorithms/graph/breadth-first-search) (BFS)
|
||||
* `B` [Jogo do Salto](src/algorithms/uncategorized/jump-game)
|
||||
* `A` [Permutações](src/algorithms/sets/permutations) (com e sem repetições)
|
||||
* `A` [Combinações](src/algorithms/sets/combinations) (com e sem repetições)
|
||||
* **Programação Dinâmica** - Criar uma solução usando sub-soluções encontradas anteriormente
|
||||
* `B` [Fibonacci Number](src/algorithms/math/fibonacci)
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game)
|
||||
* `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - Trapping problema da água da chuva
|
||||
* `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - Distância mínima de edição entre duas sequências
|
||||
* `A` [Longest Common Subsequence](src/algorithms/sets/longest-common-subsequence) (LCS)
|
||||
* `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
|
||||
* `A` [Longest Increasing Subsequence](src/algorithms/sets/longest-increasing-subsequence)
|
||||
* `A` [Shortest Common Supersequence](src/algorithms/sets/shortest-common-supersequence)
|
||||
* `A` [0/1 Knapsack Problem](src/algorithms/sets/knapsack-problem)
|
||||
* `A` [Integer Partition](src/algorithms/math/integer-partition)
|
||||
* `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
|
||||
* `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - Encontrar o caminho mais curto para todos os vértices do gráfico
|
||||
* `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - Encontrar caminhos mais curtos entre todos os pares de vértices
|
||||
* `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
|
||||
* **Backtracking** - Da mesma forma que a força bruta, tente gerar todas as soluções possíveis, mas cada vez que você gerar a próxima solução, você testará
|
||||
se satisfizer todas as condições, e só então continuar gerando soluções subseqüentes. Caso contrário, volte atrás e siga um caminho diferente para encontrar uma solução. Normalmente, a passagem DFS do espaço de estados está sendo usada.
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game)
|
||||
* `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
|
||||
* `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visite todos os vértices exatamente uma vez
|
||||
* `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
|
||||
* `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
|
||||
* `A` [Combination Sum](src/algorithms/sets/combination-sum) - Encontre todas as combinações que formam uma soma específica
|
||||
* **Branch & Bound** - Lembre-se da solução de menor custo encontrada em cada etapa do retrocesso
|
||||
pesquisar e usar o custo da solução de menor custo encontrada até o limite inferior do custo de
|
||||
* `B` [Número de Fibonacci](src/algorithms/math/fibonacci)
|
||||
* `B` [Jogo do Salto](src/algorithms/uncategorized/jump-game)
|
||||
* `B` [Caminhos Únicos](src/algorithms/uncategorized/unique-paths)
|
||||
* `B` [Terraços de Chuva](src/algorithms/uncategorized/rain-terraces) - Trapping problema da água da chuva
|
||||
* `A` [Distância Levenshtein](src/algorithms/string/levenshtein-distance) - Distância mínima de edição entre duas sequências
|
||||
* `A` [Mais Longa Subsequência Comum](src/algorithms/sets/longest-common-subsequence) (LCS)
|
||||
* `A` [Substring Comum Mais Longa](src/algorithms/string/longest-common-substring)
|
||||
* `A` [Maior Subsequência Crescente](src/algorithms/sets/longest-increasing-subsequence)
|
||||
* `A` [Supersequência Comum Mais Curta](src/algorithms/sets/shortest-common-supersequence)
|
||||
* `A` [Problema da Mochila](src/algorithms/sets/knapsack-problem)
|
||||
* `A` [Partição Inteira](src/algorithms/math/integer-partition)
|
||||
* `A` [Subarray Máximo](src/algorithms/sets/maximum-subarray)
|
||||
* `A` [Algoritmo de Bellman-Ford](src/algorithms/graph/bellman-ford) - Encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
|
||||
* `A` [Algoritmo de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - Encontrar caminhos mais curtos entre todos os pares de vértices
|
||||
* `A` [Expressões Regulares Correspondentes](src/algorithms/string/regular-expression-matching)
|
||||
* **Backtracking** - Da mesma forma que a força bruta, tente gerar todas as soluções possíveis, mas, cada vez que você gerar a próxima solução será necessário testar se a mesma satisfaz todas as condições, e só então continuará a gerar as soluções subsequentes. Caso contrário, volte atrás e siga um caminho diferente para encontrar uma solução. Normalmente, a passagem DFS do espaço de estados está sendo usada.
|
||||
* `B` [Jogo do Salto](src/algorithms/uncategorized/jump-game)
|
||||
* `B` [Caminhos Únicos](src/algorithms/uncategorized/unique-paths)
|
||||
* `A` [Ciclo Hamiltoniano](src/algorithms/graph/hamiltonian-cycle) - Visite todos os vértices exatamente uma vez
|
||||
* `A` [Problema das N-Rainhas](src/algorithms/uncategorized/n-queens)
|
||||
* `A` [Passeio do Cavaleiro](src/algorithms/uncategorized/knight-tour)
|
||||
* `A` [Soma de Combinação](src/algorithms/sets/combination-sum) - Encontre todas as combinações que formam uma soma específica
|
||||
* **Branch & Bound** - Lembre-se da solução de menor custo encontrada em cada etapa do retrocesso, pesquisar e usar o custo da solução de menor custo encontrada até o limite inferior do custo de
|
||||
solução de menor custo para o problema, a fim de descartar soluções parciais com custos maiores que o
|
||||
solução de menor custo encontrada até o momento. Normalmente, a travessia BFS em combinação com a passagem DFS do espaço de estados
|
||||
árvore está sendo usada
|
||||
@ -225,10 +222,19 @@ npm test
|
||||
```
|
||||
npm test -- 'LinkedList'
|
||||
```
|
||||
**Solução de problemas**
|
||||
|
||||
**Parque infantil**
|
||||
Caso o linting ou o teste estejam falhando, tente excluir a pasta node_modules e reinstalar os pacotes npm:
|
||||
```
|
||||
rm -rf ./node_modules
|
||||
npm i
|
||||
```
|
||||
|
||||
Você pode brincar com estruturas de dados e algoritmos em `./src/playground/playground.js` arquivar e escrever
|
||||
Verifique também se você está usando uma versão correta do Node (>=14.16.0). Se você estiver usando [nvm](https://github.com/nvm-sh/nvm) para gerenciamento de versão do Node, você pode executar `nvm use` a partir da pasta raiz do projeto e a versão correta será escolhida.
|
||||
|
||||
**Playground**
|
||||
|
||||
Você pode brincar com estruturas de dados e algoritmos no arquivo `./src/playground/playground.js` e escrever
|
||||
testes para isso em `./src/playground/__test__/playground.test.js`.
|
||||
|
||||
Em seguida, basta executar o seguinte comando para testar se o código do seu playground funciona conforme o esperado:
|
||||
@ -241,15 +247,16 @@ npm test -- 'playground'
|
||||
|
||||
### Referências
|
||||
|
||||
[▶ Estruturas de dados e algoritmos no YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [▶ Estruturas de Dados e Algoritmos no YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [✍🏻 Esboços de Estruturas de Dados](https://okso.app/showcase/data-structures)
|
||||
|
||||
### Notação Big O
|
||||
|
||||
Ordem de crescimento dos algoritmos especificados em notação Big O.
|
||||
A notação Big O é usada para classificar algoritmos de acordo com a forma como seu tempo de execução ou requisitos de espaço crescem à medida que o tamanho da entrada aumenta. No gráfico abaixo você pode encontrar as ordens mais comuns de crescimento de algoritmos especificados na notação Big O.
|
||||
|
||||

|
||||
|
||||
Fonte: [Notação Big-O dicas](http://bigocheatsheet.com/).
|
||||
Fonte: [Notação Big-O Dicas](http://bigocheatsheet.com/).
|
||||
|
||||
Abaixo está a lista de algumas das notações Big O mais usadas e suas comparações de desempenho em relação aos diferentes tamanhos dos dados de entrada.
|
||||
|
||||
@ -271,14 +278,14 @@ Abaixo está a lista de algumas das notações Big O mais usadas e suas compara
|
||||
| **Stack** | n | n | 1 | 1 | |
|
||||
| **Queue** | n | n | 1 | 1 | |
|
||||
| **Linked List** | n | n | 1 | 1 | |
|
||||
| **Hash Table** | - | n | n | n | Em caso de uma função hash perfeita, os custos seriam O (1) |
|
||||
| **Binary Search Tree** | n | n | n | n | No caso de custos de árvore equilibrados seria O (log (n))
|
||||
| **Hash Table** | - | n | n | n | Em caso de uma função hash perfeita, os custos seriam O(1) |
|
||||
| **Binary Search Tree** | n | n | n | n | No caso de custos de árvore equilibrados seria O(log(n))
|
||||
| **B-Tree** | log(n) | log(n) | log(n) | log(n) | |
|
||||
| **Red-Black Tree** | log(n) | log(n) | log(n) | log(n) | |
|
||||
| **AVL Tree** | log(n) | log(n) | log(n) | log(n) | |
|
||||
| **Bloom Filter** | - | 1 | 1 | - | Falsos positivos são possíveis durante a pesquisa |
|
||||
|
||||
### Array Sorting Algorithms Complexity
|
||||
### Complexidade dos Algoritmos de Ordenação de Matrizes
|
||||
|
||||
| Nome | Melhor | Média | Pior | Mémoria | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
@ -287,7 +294,7 @@ Abaixo está a lista de algumas das notações Big O mais usadas e suas compara
|
||||
| **Selection sort** | n<sup>2</sup> | n<sup>2</sup> | n<sup>2</sup> | 1 | Não | |
|
||||
| **Heap sort** | n log(n) | n log(n) | n log(n) | 1 | Não | |
|
||||
| **Merge sort** | n log(n) | n log(n) | n log(n) | n | Sim | |
|
||||
| **Quick sort** | n log(n) | n log(n) | n<sup>2</sup> | log(n) | Não | O Quicksort geralmente é feito no local com o espaço de pilha O O(log(n)) stack space |
|
||||
| **Quick sort** | n log(n) | n log(n) | n<sup>2</sup> | log(n) | Não | O Quicksort geralmente é feito no local com espaço de pilha O(log(n)) |
|
||||
| **Shell sort** | n log(n) | depende da sequência de lacunas | n (log(n))<sup>2</sup> | 1 | Não | |
|
||||
| **Counting sort** | n + r | n + r | n + r | n + r | Sim | r - maior número na matriz |
|
||||
| **Radix sort** | n * k | n * k | n * k | n + k | Sim | k - comprimento da chave mais longa |
|
||||
|
||||
@ -1,7 +1,8 @@
|
||||
# Reversed Linked List Traversal
|
||||
|
||||
_Read this in other languages:_
|
||||
[中文](README.zh-CN.md)
|
||||
[_中文_](README.zh-CN.md),
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
The task is to traverse the given linked list in reversed order.
|
||||
|
||||
|
||||
23
src/algorithms/linked-list/reverse-traversal/README.pt-BR.md
Normal file
23
src/algorithms/linked-list/reverse-traversal/README.pt-BR.md
Normal file
@ -0,0 +1,23 @@
|
||||
# Travessia de Lista Encadeada Reversa
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_中文_](README.zh-CN.md),
|
||||
[_English_](README.md)
|
||||
|
||||
A tarefa é percorrer a lista encadeada fornecida em ordem inversa.
|
||||
|
||||
Por exemplo, para a seguinte lista vinculada:
|
||||
|
||||

|
||||
|
||||
A ordem de travessia deve ser:
|
||||
|
||||
```texto
|
||||
37 → 99 → 12
|
||||
```
|
||||
|
||||
A complexidade de tempo é `O(n)` porque visitamos cada nó apenas uma vez.
|
||||
|
||||
## Referência
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
|
||||
@ -2,7 +2,8 @@
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Русский_](README.ru-RU.md),
|
||||
[中文](README.zh-CN.md)
|
||||
[_中文_](README.zh-CN.md),
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
The task is to traverse the given linked list in straight order.
|
||||
|
||||
|
||||
24
src/algorithms/linked-list/traversal/README.pt-BR.md
Normal file
24
src/algorithms/linked-list/traversal/README.pt-BR.md
Normal file
@ -0,0 +1,24 @@
|
||||
# Travessia de Lista Encadeada
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_Русский_](README.ru-RU.md),
|
||||
[_中文_](README.zh-CN.md),
|
||||
[_English_](README.md)
|
||||
|
||||
A tarefa é percorrer a lista encadeada fornecida em ordem direta.
|
||||
|
||||
Por exemplo, para a seguinte lista vinculada:
|
||||
|
||||

|
||||
|
||||
A ordem de travessia deve ser:
|
||||
|
||||
```texto
|
||||
12 → 99 → 37
|
||||
```
|
||||
|
||||
A complexidade de tempo é `O(n)` porque visitamos cada nó apenas uma vez.
|
||||
|
||||
## Referência
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
|
||||
@ -1,5 +1,8 @@
|
||||
# k-Means Algorithm
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
The **k-Means algorithm** is an unsupervised Machine Learning algorithm. It's a clustering algorithm, which groups the sample data on the basis of similarity between dimensions of vectors.
|
||||
|
||||
In k-Means classification, the output is a set of classes assigned to each vector. Each cluster location is continuously optimized in order to get the accurate locations of each cluster such that they represent each group clearly.
|
||||
|
||||
35
src/algorithms/ml/k-means/README.pt-BR.md
Normal file
35
src/algorithms/ml/k-means/README.pt-BR.md
Normal file
@ -0,0 +1,35 @@
|
||||
# Algoritmo k-Means
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
O **algoritmo k-Means** é um algoritmo de aprendizado de máquina não supervisionado. É um algoritmo de agrupamento, que agrupa os dados da amostra com base na semelhança entre as dimensões dos vetores.
|
||||
|
||||
Na classificação k-Means, a saída é um conjunto de classes atribuídas a cada vetor. Cada localização de cluster é continuamente otimizada para obter as localizações precisas de cada cluster de forma que representem cada grupo claramente.
|
||||
|
||||
A ideia é calcular a similaridade entre a localização do cluster e os vetores de dados e reatribuir os clusters com base nela. [Distância Euclidiana](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/euclidean-distance) é usado principalmente para esta tarefa.
|
||||
|
||||

|
||||
|
||||
_Fonte: [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_distance)_
|
||||
|
||||
O algoritmo é o seguinte:
|
||||
|
||||
1. Verifique se há erros como dados inválidos/inconsistentes
|
||||
2. Inicialize os locais do cluster `k` com pontos `k` iniciais/aleatórios
|
||||
3. Calcule a distância de cada ponto de dados de cada cluster
|
||||
4. Atribua o rótulo do cluster de cada ponto de dados igual ao do cluster em sua distância mínima
|
||||
5. Calcule o centroide de cada cluster com base nos pontos de dados que ele contém
|
||||
6. Repita cada uma das etapas acima até que as localizações do centroide estejam variando
|
||||
|
||||
Aqui está uma visualização do agrupamento k-Means para melhor compreensão:
|
||||
|
||||

|
||||
|
||||
_Fonte: [Wikipedia](https://en.wikipedia.org/wiki/K-means_clustering)_
|
||||
|
||||
Os centroides estão se movendo continuamente para criar uma melhor distinção entre os diferentes conjuntos de pontos de dados. Como podemos ver, após algumas iterações, a diferença de centroides é bastante baixa entre as iterações. Por exemplo, entre as iterações `13` e `14` a diferença é bem pequena porque o otimizador está ajustando os casos limite.
|
||||
|
||||
## Referências
|
||||
|
||||
- [k-Means neighbors algorithm on Wikipedia](https://en.wikipedia.org/wiki/K-means_clustering)
|
||||
@ -1,5 +1,8 @@
|
||||
# k-Nearest Neighbors Algorithm
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
The **k-nearest neighbors algorithm (k-NN)** is a supervised Machine Learning algorithm. It's a classification algorithm, determining the class of a sample vector using a sample data.
|
||||
|
||||
In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its `k` nearest neighbors (`k` is a positive integer, typically small). If `k = 1`, then the object is simply assigned to the class of that single nearest neighbor.
|
||||
|
||||
44
src/algorithms/ml/knn/README.pt-BR.md
Normal file
44
src/algorithms/ml/knn/README.pt-BR.md
Normal file
@ -0,0 +1,44 @@
|
||||
# Algoritmo de k-vizinhos mais próximos
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
O **algoritmo de k-vizinhos mais próximos (k-NN)** é um algoritmo de aprendizado de máquina supervisionado. É um algoritmo de classificação, determinando a classe de um vetor de amostra usando dados de amostra.
|
||||
|
||||
Na classificação k-NN, a saída é uma associação de classe. Um objeto é classificado por uma pluralidade de votos de seus vizinhos, com o objeto sendo atribuído à classe mais comum entre seus `k` vizinhos mais próximos (`k` é um inteiro positivo, tipicamente pequeno). Se `k = 1`, então o objeto é simplesmente atribuído à classe daquele único vizinho mais próximo.
|
||||
|
||||
The idea is to calculate the similarity between two data points on the basis of a distance metric. [Distância Euclidiana](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/euclidean-distance) é usado principalmente para esta tarefa.
|
||||
|
||||

|
||||
|
||||
_Fonte: [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_distance)_
|
||||
|
||||
O algoritmo é o seguinte:
|
||||
|
||||
1. Verifique se há erros como dados/rótulos inválidos.
|
||||
2. Calcule a distância euclidiana de todos os pontos de dados nos dados de treinamento com o ponto de classificação
|
||||
3. Classifique as distâncias dos pontos junto com suas classes em ordem crescente
|
||||
4. Pegue as classes iniciais `K` e encontre o modo para obter a classe mais semelhante
|
||||
5. Informe a classe mais semelhante
|
||||
|
||||
Aqui está uma visualização da classificação k-NN para melhor compreensão:
|
||||
|
||||

|
||||
|
||||
_Fonte: [Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)_
|
||||
|
||||
A amostra de teste (ponto verde) deve ser classificada em quadrados azuis ou em triângulos vermelhos. Se `k = 3` (círculo de linha sólida) é atribuído aos triângulos vermelhos porque existem `2` triângulos e apenas `1` quadrado dentro do círculo interno. Se `k = 5` (círculo de linha tracejada) é atribuído aos quadrados azuis (`3` quadrados vs. `2` triângulos dentro do círculo externo).
|
||||
|
||||
Outro exemplo de classificação k-NN:
|
||||
|
||||
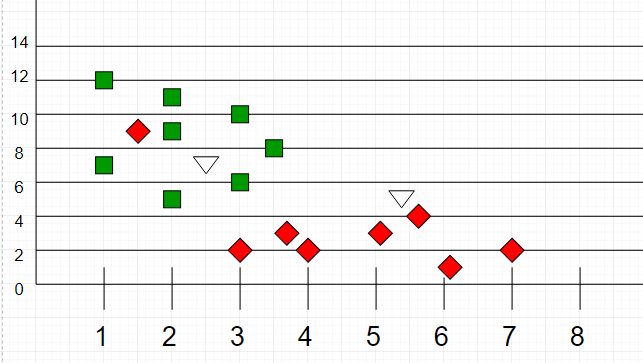
|
||||
|
||||
_Fonte: [GeeksForGeeks](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)_
|
||||
|
||||
Aqui, como podemos ver, a classificação dos pontos desconhecidos será julgada pela proximidade com outros pontos.
|
||||
|
||||
É importante notar que `K` é preferível ter valores ímpares para desempate. Normalmente `K` é tomado como `3` ou `5`.
|
||||
|
||||
## Referências
|
||||
|
||||
- [k-nearest neighbors algorithm on Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)
|
||||
@ -1,16 +1,19 @@
|
||||
# Bubble Sort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
O bubble sort, ou ordenação por flutuação (literalmente "por bolha"), é um algoritmo de ordenação dos mais simples. A ideia é percorrer o vetor diversas vezes, e a cada passagem fazer flutuar para o topo o maior elemento da sequência. Essa movimentação lembra a forma como as bolhas em um tanque de água procuram seu próprio nível, e disso vem o nome do algoritmo.
|
||||
|
||||

|
||||
|
||||
## Complexity
|
||||
## Complexidade
|
||||
|
||||
| Name | Best | Average | Worst | Memory | Stable | Comments |
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Bubble sort** | n | n<sup>2</sup> | n<sup>2</sup> | 1 | Yes | |
|
||||
| **Bubble sort** | n | n<sup>2</sup> | n<sup>2</sup> | 1 | Sim | |
|
||||
|
||||
## References
|
||||
## Referências
|
||||
|
||||
- [Wikipedia](https://pt.wikipedia.org/wiki/Bubble_sort)
|
||||
- [YouTube](https://www.youtube.com/watch?v=6Gv8vg0kcHc&index=27&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
|
||||
@ -1,5 +1,8 @@
|
||||
# Counting Sort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
In computer science, **counting sort** is an algorithm for sorting
|
||||
a collection of objects according to keys that are small integers;
|
||||
that is, it is an integer sorting algorithm. It operates by
|
||||
|
||||
70
src/algorithms/sorting/counting-sort/README.pt-br.md
Normal file
70
src/algorithms/sorting/counting-sort/README.pt-br.md
Normal file
@ -0,0 +1,70 @@
|
||||
# Counting Sort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
Em ciência da computação, **counting sort** é um algoritmo para ordenar
|
||||
uma coleção de objetos de acordo com chaves que são pequenos inteiros;
|
||||
ou seja, é um algoritmo de ordenação de inteiros. Ele opera por
|
||||
contando o número de objetos que têm cada valor de chave distinto,
|
||||
e usando aritmética nessas contagens para determinar as posições
|
||||
de cada valor de chave na sequência de saída. Seu tempo de execução é
|
||||
linear no número de itens e a diferença entre o
|
||||
valores de chave máximo e mínimo, portanto, é adequado apenas para
|
||||
uso em situações em que a variação de tonalidades não é significativamente
|
||||
maior que o número de itens. No entanto, muitas vezes é usado como
|
||||
sub-rotina em outro algoritmo de ordenação, radix sort, que pode
|
||||
lidar com chaves maiores de forma mais eficiente.
|
||||
|
||||
Como a classificação por contagem usa valores-chave como índices em um vetor,
|
||||
não é uma ordenação por comparação, e o limite inferior `Ω(n log n)` para
|
||||
a ordenação por comparação não se aplica a ele. A classificação por bucket pode ser usada
|
||||
para muitas das mesmas tarefas que a ordenação por contagem, com um tempo semelhante
|
||||
análise; no entanto, em comparação com a classificação por contagem, a classificação por bucket requer
|
||||
listas vinculadas, arrays dinâmicos ou uma grande quantidade de pré-alocados
|
||||
memória para armazenar os conjuntos de itens dentro de cada bucket, enquanto
|
||||
A classificação por contagem armazena um único número (a contagem de itens)
|
||||
por balde.
|
||||
|
||||
A classificação por contagem funciona melhor quando o intervalo de números para cada
|
||||
elemento do vetor é muito pequeno.
|
||||
|
||||
## Algoritmo
|
||||
|
||||
**Passo I**
|
||||
|
||||
Na primeira etapa, calculamos a contagem de todos os elementos do
|
||||
vetor de entrada 'A'. Em seguida, armazene o resultado no vetor de contagem `C`.
|
||||
A maneira como contamos é descrita abaixo.
|
||||
|
||||
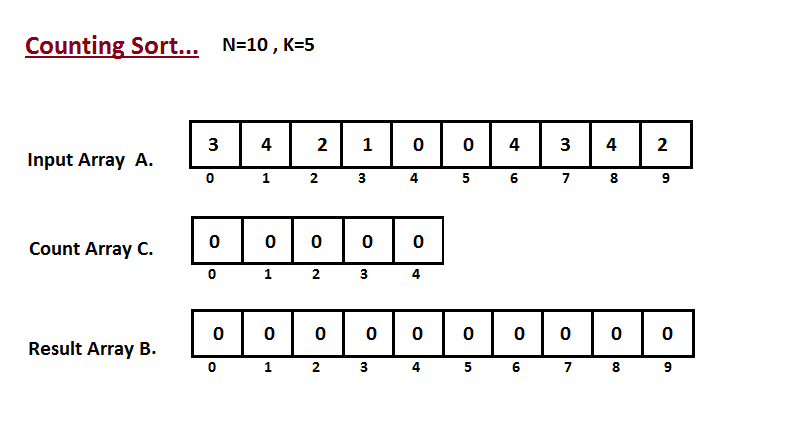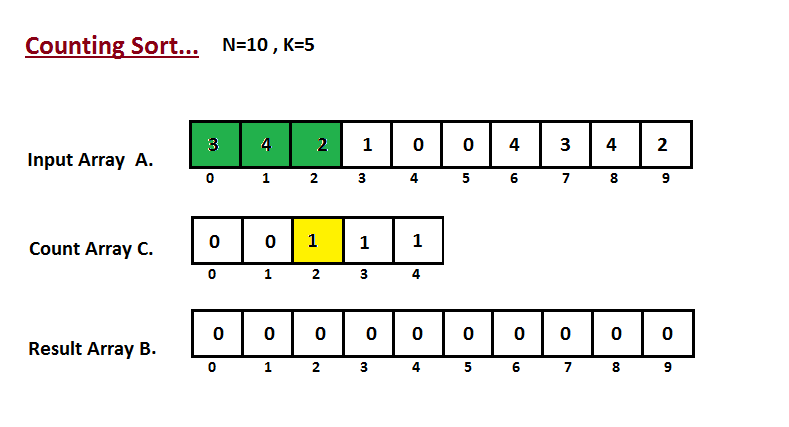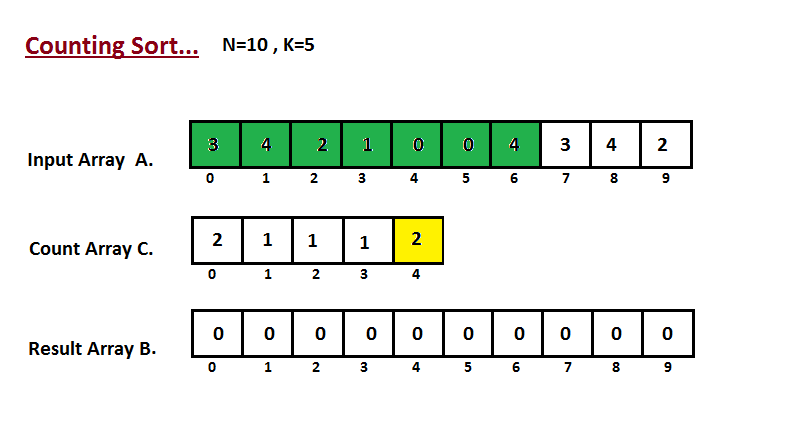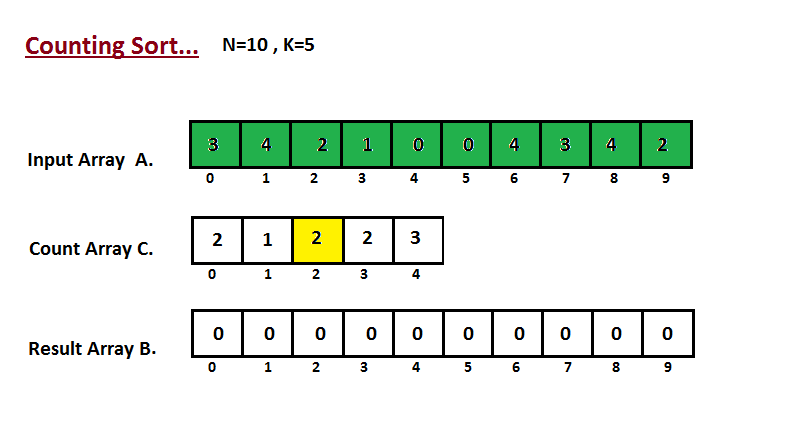
|
||||
|
||||
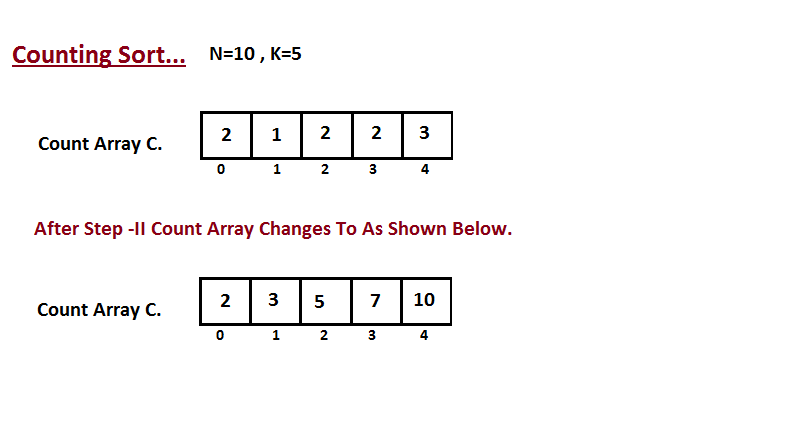
**Passo II**
|
||||
|
||||
Na segunda etapa, calculamos quantos elementos existem na entrada
|
||||
do vetor `A` que são menores ou iguais para o índice fornecido.
|
||||
`Ci` = números de elementos menores ou iguais a `i` no vetor de entrada.
|
||||
|
||||
|
||||
|
||||
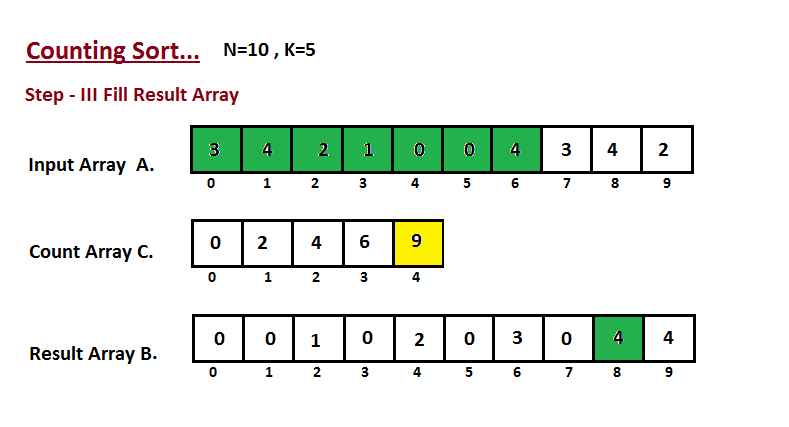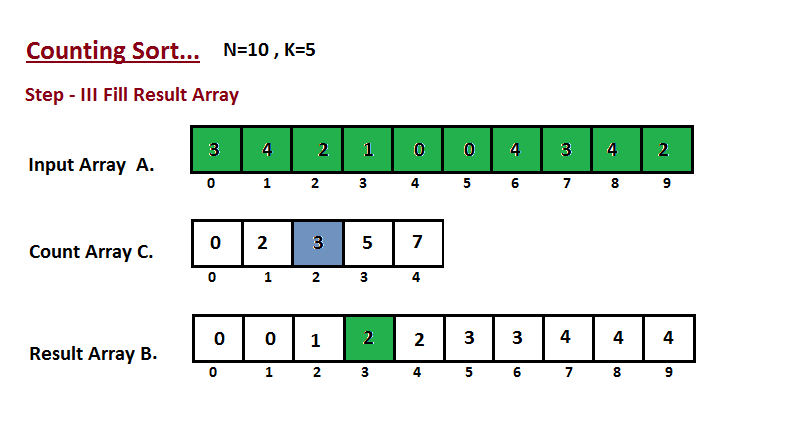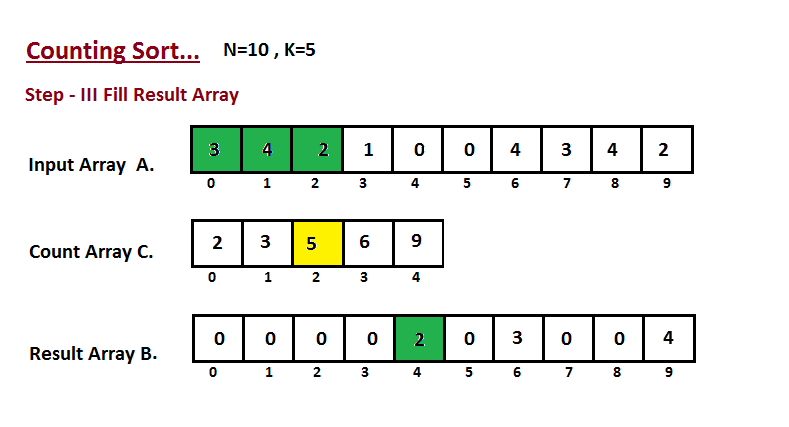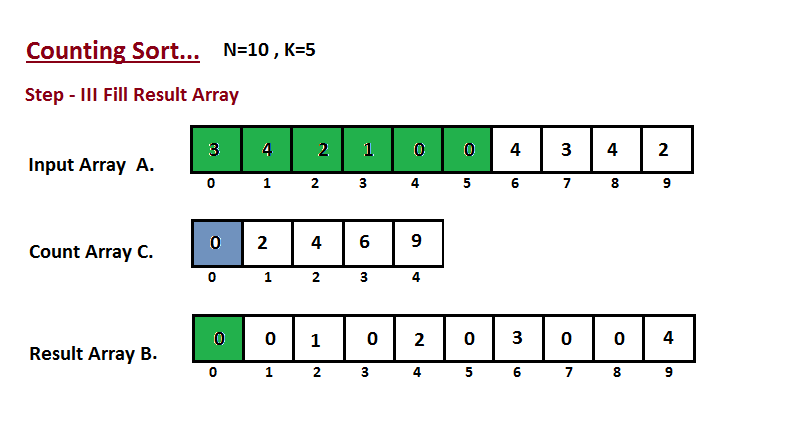
**Passo III**
|
||||
|
||||
Nesta etapa, colocamos o elemento `A` do vetor de entrada em classificado
|
||||
posição usando a ajuda do vetor de contagem construída `C`, ou seja, o que
|
||||
construímos no passo dois. Usamos o vetor de resultados `B` para armazenar
|
||||
os elementos ordenados. Aqui nós lidamos com o índice de `B` começando de
|
||||
zero.
|
||||
|
||||
|
||||
|
||||
## Complexidade
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Counting sort** | n + r | n + r | n + r | n + r | Sim | r - Maior número no vetor |
|
||||
|
||||
## Referências
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Counting_sort)
|
||||
- [YouTube](https://www.youtube.com/watch?v=OKd534EWcdk&index=61&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [EfficientAlgorithms](https://efficientalgorithms.blogspot.com/2016/09/lenear-sorting-counting-sort.html)
|
||||
@ -1,5 +1,8 @@
|
||||
# Heap Sort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
Heapsort is a comparison-based sorting algorithm.
|
||||
Heapsort can be thought of as an improved selection
|
||||
sort: like that algorithm, it divides its input into
|
||||
|
||||
20
src/algorithms/sorting/heap-sort/README.pt-BR.md
Normal file
20
src/algorithms/sorting/heap-sort/README.pt-BR.md
Normal file
@ -0,0 +1,20 @@
|
||||
# Heap Sort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
Heapsort é um algoritmo de ordenação baseado em comparação. O Heapsort pode ser pensado como uma seleção aprimorada sort: como esse algoritmo, ele divide sua entrada em uma região classificada e uma região não classificada, e iterativamente encolhe a região não classificada extraindo o maior elemento e movendo-o para a região classificada. A melhoria consiste no uso de uma estrutura de dados heap em vez de uma busca em tempo linear para encontrar o máximo.
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
## Complexidade
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Heap sort** | n log(n) | n log(n) | n log(n) | 1 | Não | |
|
||||
|
||||
## Referências
|
||||
|
||||
[Wikipedia](https://en.wikipedia.org/wiki/Heapsort)
|
||||
@ -1,5 +1,8 @@
|
||||
# Insertion Sort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
Insertion sort is a simple sorting algorithm that builds
|
||||
the final sorted array (or list) one item at a time.
|
||||
It is much less efficient on large lists than more
|
||||
|
||||
22
src/algorithms/sorting/insertion-sort/README.pt-BR.md
Normal file
22
src/algorithms/sorting/insertion-sort/README.pt-BR.md
Normal file
@ -0,0 +1,22 @@
|
||||
# Insertion Sort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
A ordenação por inserção é um algoritmo de ordenação simples que criaa matriz classificada final (ou lista) um item de cada vez.
|
||||
É muito menos eficiente em grandes listas do que mais algoritmos avançados, como quicksort, heapsort ou merge
|
||||
ordenar.
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
## Complexidade
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Insertion sort** | n | n<sup>2</sup> | n<sup>2</sup> | 1 | Sim | |
|
||||
|
||||
## Referências
|
||||
|
||||
[Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort)
|
||||
@ -1,7 +1,8 @@
|
||||
# Merge Sort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_한국어_](README.ko-KR.md)
|
||||
[_한국어_](README.ko-KR.md),
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
In computer science, merge sort (also commonly spelled
|
||||
mergesort) is an efficient, general-purpose,
|
||||
|
||||
38
src/algorithms/sorting/merge-sort/README.pt-BR.md
Normal file
38
src/algorithms/sorting/merge-sort/README.pt-BR.md
Normal file
@ -0,0 +1,38 @@
|
||||
# Merge Sort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_한국어_](README.ko-KR.md),
|
||||
[_English_](README.md)
|
||||
|
||||
Em ciência da computação, merge sort (também comumente escrito
|
||||
mergesort) é uma ferramenta eficiente, de propósito geral,
|
||||
algoritmo de ordenação baseado em comparação. A maioria das implementações
|
||||
produzir uma classificação estável, o que significa que a implementação
|
||||
preserva a ordem de entrada de elementos iguais na ordenação
|
||||
resultado. Mergesort é um algoritmo de divisão e conquista que
|
||||
foi inventado por John von Neumann em 1945.
|
||||
|
||||
Um exemplo de classificação de mesclagem. Primeiro divida a lista em
|
||||
a menor unidade (1 elemento), então compare cada
|
||||
elemento com a lista adjacente para classificar e mesclar o
|
||||
duas listas adjacentes. Finalmente todos os elementos são ordenados
|
||||
e mesclado.
|
||||
|
||||

|
||||
|
||||
Um algoritmo de classificação de mesclagem recursivo usado para classificar uma matriz de 7
|
||||
valores inteiros. Estes são os passos que um ser humano daria para
|
||||
emular merge sort (top-down).
|
||||
|
||||

|
||||
|
||||
## Complexidade
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Merge sort** | n log(n) | n log(n) | n log(n) | n | Sim | |
|
||||
|
||||
## Referências
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Merge_sort)
|
||||
- [YouTube](https://www.youtube.com/watch?v=KF2j-9iSf4Q&index=27&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
@ -1,8 +1,8 @@
|
||||
# Quicksort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md),
|
||||
[_简体中文_](README.zh-CN.md)
|
||||
[_简体中文_](README.zh-CN.md),
|
||||
[_Português_](README.pt-BR.md)
|
||||
|
||||
Quicksort is a divide and conquer algorithm.
|
||||
Quicksort first divides a large array into two smaller
|
||||
|
||||
@ -1,15 +1,19 @@
|
||||
# Quicksort
|
||||
|
||||
Quicksort é um algoritmo de dividir para conquistar é um algoritmo de divisão e conquista.
|
||||
_Leia isso em outros idiomas:_
|
||||
[_简体中文_](README.zh-CN.md),
|
||||
[_English_](README.md)
|
||||
|
||||
Quicksort é um algoritmo de dividir para conquistar.
|
||||
Quicksort primeiro divide uma grande matriz em duas menores
|
||||
submatrizes: os elementos baixos e os elementos altos.
|
||||
O Quicksort pode então classificar recursivamente as submatrizes
|
||||
O Quicksort pode então classificar recursivamente as submatrizes.
|
||||
|
||||
As etapas são:
|
||||
|
||||
1. Escolha um elemento, denominado pivô, na matriz.
|
||||
2. Particionamento: reordene a matriz para que todos os elementos com
|
||||
valores menores que o pivô vêm antes do pivô, enquanto todos
|
||||
valores menores que o pivô estejam antes do pivô, enquanto todos
|
||||
elementos com valores maiores do que o pivô vêm depois dele
|
||||
(valores iguais podem ser usados em qualquer direção). Após este particionamento,
|
||||
o pivô está em sua posição final. Isso é chamado de
|
||||
@ -27,7 +31,7 @@ As linhas horizontais são valores dinâmicos.
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Quick sort** | n log(n) | n log(n) | n<sup>2</sup> | log(n) | No | Quicksort geralmente é feito no local com espaço de pilha O(log(n)) |
|
||||
| **Quick sort** | n log(n) | n log(n) | n<sup>2</sup> | log(n) | Não | Quicksort geralmente é feito no local com espaço de pilha O(log(n)) |
|
||||
|
||||
## Referências
|
||||
|
||||
|
||||
@ -1,5 +1,8 @@
|
||||
# Radix Sort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md),
|
||||
|
||||
In computer science, **radix sort** is a non-comparative integer sorting
|
||||
algorithm that sorts data with integer keys by grouping keys by the individual
|
||||
digits which share the same significant position and value. A positional notation
|
||||
|
||||
48
src/algorithms/sorting/radix-sort/README.pt-BR.md
Normal file
48
src/algorithms/sorting/radix-sort/README.pt-BR.md
Normal file
@ -0,0 +1,48 @@
|
||||
# Radix Sort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md)
|
||||
|
||||
Em ciência da computação, **radix sort** é uma classificação inteira não comparativa
|
||||
algoritmo que classifica os dados com chaves inteiras agrupando as chaves pelo indivíduo
|
||||
dígitos que compartilham a mesma posição e valor significativos. Uma notação posicional
|
||||
é necessário, mas porque os números inteiros podem representar cadeias de caracteres
|
||||
(por exemplo, nomes ou datas) e números de ponto flutuante especialmente formatados, base
|
||||
sort não está limitado a inteiros.
|
||||
|
||||
*De onde vem o nome?*
|
||||
|
||||
Em sistemas numéricos matemáticos, a *radix* ou base é o número de dígitos únicos,
|
||||
incluindo o dígito zero, usado para representar números em um sistema de numeração posicional.
|
||||
Por exemplo, um sistema binário (usando números 0 e 1) tem uma raiz de 2 e um decimal
|
||||
sistema (usando números de 0 a 9) tem uma raiz de 10.
|
||||
|
||||
## Eficiência
|
||||
|
||||
O tópico da eficiência do radix sort comparado a outros algoritmos de ordenação é
|
||||
um pouco complicado e sujeito a muitos mal-entendidos. Se raiz
|
||||
sort é igualmente eficiente, menos eficiente ou mais eficiente do que o melhor
|
||||
algoritmos baseados em comparação depende dos detalhes das suposições feitas.
|
||||
A complexidade de classificação de raiz é `O(wn)` para chaves `n` que são inteiros de tamanho de palavra `w`.
|
||||
Às vezes, `w` é apresentado como uma constante, o que tornaria a classificação radix melhor
|
||||
(para `n` suficientemente grande) do que os melhores algoritmos de ordenação baseados em comparação,
|
||||
que todos realizam comparações `O(n log n)` para classificar chaves `n`. No entanto, em
|
||||
geral `w` não pode ser considerado uma constante: se todas as chaves `n` forem distintas,
|
||||
então `w` tem que ser pelo menos `log n` para que uma máquina de acesso aleatório seja capaz de
|
||||
armazená-los na memória, o que dá na melhor das hipóteses uma complexidade de tempo `O(n log n)`. Este
|
||||
parece tornar a ordenação radix no máximo tão eficiente quanto a melhor
|
||||
ordenações baseadas em comparação (e pior se as chaves forem muito mais longas que `log n`).
|
||||
|
||||

|
||||
|
||||
## Complexidade
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Radix sort** | n * k | n * k | n * k | n + k | Sim | k - comprimento da chave mais longa |
|
||||
|
||||
## Referências
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Radix_sort)
|
||||
- [YouTube](https://www.youtube.com/watch?v=XiuSW_mEn7g&index=62&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [ResearchGate](https://www.researchgate.net/figure/Simplistic-illustration-of-the-steps-performed-in-a-radix-sort-In-this-example-the_fig1_291086231)
|
||||
@ -1,7 +1,7 @@
|
||||
# Selection Sort
|
||||
|
||||
_Read this in other languages:_
|
||||
[Português brasileiro](README.pt-BR.md).
|
||||
[_Português_](README.pt-BR.md).
|
||||
|
||||
Selection sort is a sorting algorithm, specifically an
|
||||
in-place comparison sort. It has O(n2) time complexity,
|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
# Selection Sort
|
||||
|
||||
_Leia isso em outras línguas:_
|
||||
[english](README.md).
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md).
|
||||
|
||||
Selection Sort é um algoritmo de ordenação, mais especificamente um algoritmo de ordenação por comparação in-place (requer uma quantidade constante de espaço de memória adicional). Tem complexidade O(n²), tornando-o ineficiente em listas grandes e, geralmente, tem desempenho inferior ao similar Insertion Sort. O Selection Sort é conhecido por sua simplicidade e tem vantagens de desempenho sobre algoritmos mais complexos em certas situações, particularmente quando a memória auxiliar é limitada.
|
||||
|
||||
|
||||
@ -1,5 +1,8 @@
|
||||
# Shellsort
|
||||
|
||||
_Read this in other languages:_
|
||||
[_Português_](README.pt-BR.md).
|
||||
|
||||
Shellsort, also known as Shell sort or Shell's method,
|
||||
is an in-place comparison sort. It can be seen as either a
|
||||
generalization of sorting by exchange (bubble sort) or sorting
|
||||
|
||||
60
src/algorithms/sorting/shell-sort/README.pt-BR.md
Normal file
60
src/algorithms/sorting/shell-sort/README.pt-BR.md
Normal file
@ -0,0 +1,60 @@
|
||||
# Shellsort
|
||||
|
||||
_Leia isso em outros idiomas:_
|
||||
[_English_](README.md).
|
||||
|
||||
Shellsort, também conhecido como Shell sort ou método de Shell,
|
||||
é uma classificação de comparação in-loco. Pode ser visto tanto como um
|
||||
generalização da ordenação por troca (bubble sort) ou ordenação
|
||||
por inserção (ordenação por inserção). O método começa classificando
|
||||
pares de elementos distantes um do outro, então progressivamente
|
||||
reduzindo a distância entre os elementos a serem comparados. Iniciando
|
||||
com elementos distantes, pode mover alguns fora do lugar
|
||||
elementos em posição mais rápido do que um simples vizinho mais próximo
|
||||
intercâmbio
|
||||
|
||||

|
||||
|
||||
## Como o Shellsort funciona?
|
||||
|
||||
Para nosso exemplo e facilidade de compreensão, tomamos o intervalo
|
||||
de `4`. Faça uma sub-lista virtual de todos os valores localizados no
|
||||
intervalo de 4 posições. Aqui esses valores são
|
||||
`{35, 14}`, `{33, 19}`, `{42, 27}` e `{10, 44}`
|
||||
|
||||

|
||||
|
||||
Comparamos valores em cada sublista e os trocamos (se necessário)
|
||||
na matriz original. Após esta etapa, o novo array deve
|
||||
parece com isso
|
||||
|
||||

|
||||
|
||||
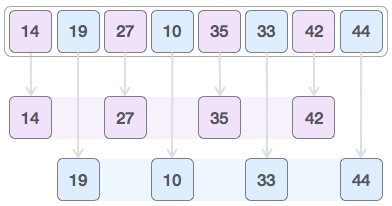
Então, pegamos o intervalo de 2 e essa lacuna gera duas sub-listas
|
||||
- `{14, 27, 35, 42}`, `{19, 10, 33, 44}`
|
||||
|
||||
|
||||
|
||||
Comparamos e trocamos os valores, se necessário, no array original.
|
||||
Após esta etapa, a matriz deve ficar assim
|
||||
|
||||

|
||||
|
||||
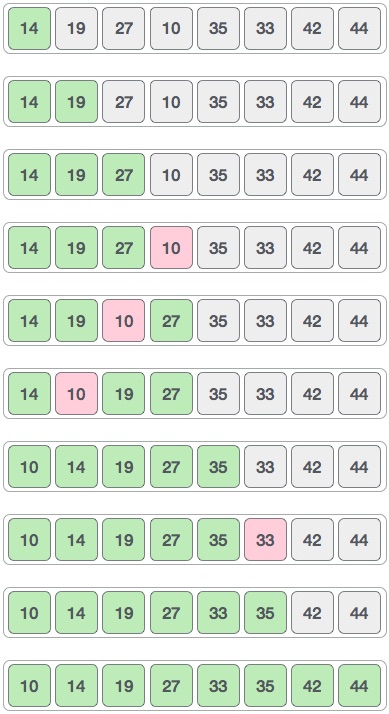
> OBS: Na imagem abaixo há um erro de digitação e a matriz de resultados deve ser `[14, 10, 27, 19, 35, 33, 42, 44]`.
|
||||
|
||||
Finalmente, ordenamos o resto do array usando o intervalo de valor 1.
|
||||
A classificação de shell usa a classificação por inserção para classificar a matriz.
|
||||
|
||||
|
||||
|
||||
## Complexidade
|
||||
|
||||
| Nome | Melhor | Média | Pior | Memória | Estável | Comentários |
|
||||
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||
| **Shell sort** | n log(n) | depends on gap sequence | n (log(n))<sup>2</sup> | 1 | Não | |
|
||||
|
||||
## Referências
|
||||
|
||||
- [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/shell_sort_algorithm.htm)
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Shellsort)
|
||||
- [YouTube by Rob Edwards](https://www.youtube.com/watch?v=ddeLSDsYVp8&index=79&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
@ -3,7 +3,7 @@
|
||||
O **bloom filter** é uma estrutura de dados probabilística
|
||||
espaço-eficiente designada para testar se um elemento está
|
||||
ou não presente em um conjunto de dados. Foi projetado para ser
|
||||
incrivelmente rápido e utilizar o mínimo de memória ao
|
||||
incrivelmente rápida e utilizar o mínimo de memória ao
|
||||
potencial custo de um falso-positivo. Correspondências
|
||||
_falsas positivas_ são possíveis, contudo _falsos negativos_
|
||||
não são - em outras palavras, a consulta retorna
|
||||
@ -12,7 +12,7 @@ não são - em outras palavras, a consulta retorna
|
||||
Bloom propôs a técnica para aplicações onde a quantidade
|
||||
de entrada de dados exigiria uma alocação de memória
|
||||
impraticavelmente grande se as "convencionais" técnicas
|
||||
error-free hashing fossem aplicado.
|
||||
error-free hashing fossem aplicadas.
|
||||
|
||||
## Descrição do algoritmo
|
||||
|
||||
|
||||
@ -1,8 +1,8 @@
|
||||
# Conjunto Disjuntor (Disjoint Set)
|
||||
# Conjunto Disjunto (Disjoint Set)
|
||||
|
||||
**Conjunto Disjuntor**
|
||||
**Conjunto Disjunto**
|
||||
|
||||
**Conjunto Disjuntor** é uma estrutura de dados (também chamado de
|
||||
**Conjunto Disjunto** é uma estrutura de dados (também chamado de
|
||||
estrutura de dados de union–find ou merge–find) é uma estrutura de dados
|
||||
que rastreia um conjunto de elementos particionados em um número de
|
||||
subconjuntos separados (sem sobreposição).
|
||||
@ -10,9 +10,9 @@ Ele fornece operações de tempo quase constante (limitadas pela função
|
||||
inversa de Ackermann) para *adicionar novos conjuntos*, para
|
||||
*mesclar/fundir conjuntos existentes* e para *determinar se os elementos
|
||||
estão no mesmo conjunto*.
|
||||
Além de muitos outros usos (veja a seção Applications), conjunto disjuntor
|
||||
Além de muitos outros usos (veja a seção Applications), conjuntos disjuntos
|
||||
desempenham um papel fundamental no algoritmo de Kruskal para encontrar a
|
||||
árvore geradora mínima de um gráfico (graph).
|
||||
árvore geradora mínima de um grafo (graph).
|
||||
|
||||

|
||||
|
||||
|
||||
@ -4,7 +4,7 @@ Na ciência da computação, uma **lista duplamente conectada** é uma estrutura
|
||||
de dados vinculada que se consistem em um conjunto de registros
|
||||
sequencialmente vinculados chamados de nós (nodes). Em cada nó contém dois
|
||||
campos, chamados de ligações, que são referenciados ao nó anterior e posterior
|
||||
de uma sequência de nós. O começo e o fim dos nós anteriormente e posteiormente
|
||||
de uma sequência de nós. O começo e o fim dos nós anteriormente e posteriormente
|
||||
ligados, respectiviamente, apontam para algum tipo de terminação, normalmente
|
||||
um nó sentinela ou nulo, para facilitar a travessia da lista. Se existe
|
||||
somente um nó sentinela, então a lista é ligada circularmente através do nó
|
||||
@ -20,7 +20,7 @@ Enquanto adicionar ou remover um nó de uma lista duplamente vinculada requer
|
||||
alterar mais ligações (conexões) do que em uma lista encadeada individualmente
|
||||
(singly linked list), as operações são mais simples e potencialmente mais
|
||||
eficientes (para nós que não sejam nós iniciais) porque não há necessidade
|
||||
de se manter rastreamento do nó anterior durante a travessia ou não há
|
||||
de manter um rastreamento do nó anterior durante a travessia ou não há
|
||||
necessidade de percorrer a lista para encontrar o nó anterior, para que
|
||||
então sua ligação/conexão possa ser modificada.
|
||||
|
||||
@ -44,7 +44,7 @@ Add(value)
|
||||
end Add
|
||||
```
|
||||
|
||||
### Deletar
|
||||
### Remoção
|
||||
|
||||
```text
|
||||
Remove(head, value)
|
||||
|
||||
@ -1,6 +1,6 @@
|
||||
# Tabela de Hash (Hash Table)
|
||||
|
||||
Na ciência da computação, uma **tabela de hash** (hash map) é uma
|
||||
Na ciência da computação, uma **tabela de hash** (hash table) é uma
|
||||
estrutura de dados pela qual implementa um tipo de dado abstrado de
|
||||
*array associativo*, uma estrutura que pode *mapear chaves para valores*.
|
||||
Uma tabela de hash utiliza uma *função de hash* para calcular um índice
|
||||
@ -10,7 +10,7 @@ pode ser encontrado.
|
||||
Idealmente, a função de hash irá atribuir a cada chave a um bucket único,
|
||||
mas a maioria dos designs de tabela de hash emprega uma função de hash
|
||||
imperfeita, pela qual poderá causar colisões de hashes onde a função de hash
|
||||
gera o mesmo índice para mais de uma chave.Tais colisões devem ser
|
||||
gera o mesmo índice para mais de uma chave. Tais colisões devem ser
|
||||
acomodados de alguma forma.
|
||||
|
||||

|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
# Fila de Prioridade (Priority Queue)
|
||||
|
||||
Na ciência da computação, uma **fila de prioridade** é um tipo de dados
|
||||
abastrato que é como uma fila regular (regular queue) ou estrutura de
|
||||
Na ciência da computação, uma **fila de prioridade** é um tipo de estrutura de
|
||||
dados abastrata que é como uma fila regular (regular queue) ou estrutura de
|
||||
dados de pilha (stack), mas adicionalmente cada elemento possui uma
|
||||
"prioridade" associada.
|
||||
|
||||
@ -10,11 +10,11 @@ antes de um elemento com baixa prioridade. Caso dois elementos posusam a
|
||||
mesma prioridade, eles serão servidos de acordo com sua ordem na fila.
|
||||
|
||||
Enquanto as filas de prioridade são frequentemente implementadas com
|
||||
pilhas (heaps), elas são conceitualmente distintas das pilhas (heaps).
|
||||
pilhas (stacks), elas são conceitualmente distintas das pilhas (stacks).
|
||||
A fila de prioridade é um conceito abstrato como uma "lista" (list) ou
|
||||
um "mapa" (map); assim como uma lista pode ser implementada com uma
|
||||
lista encadeada (liked list) ou um array, a fila de prioridade pode ser
|
||||
implementada com uma pilha (heap) ou com uima variedade de outros métodos,
|
||||
implementada com uma pilha (stack) ou com uma variedade de outros métodos,
|
||||
como um array não ordenado (unordered array).
|
||||
|
||||
## Referências
|
||||
|
||||
@ -1,14 +1,14 @@
|
||||
# Stack
|
||||
# Pilha (Stack)
|
||||
|
||||
Na ciência da computação, um **stack** é uma estrutura de dados abstrata
|
||||
Na ciência da computação, uma **pilha** é uma estrutura de dados abstrata
|
||||
que serve como uma coleção de elementos com duas operações principais:
|
||||
|
||||
* **push**, pela qual adiciona um elemento à coleção, e
|
||||
* **pop**, pela qual remove o último elemento adicionado.
|
||||
|
||||
A ordem em que os elementos saem de um _stack_ dá origem ao seu
|
||||
nome alternativo, LIFO (last in, first out). Adicionalmente, uma
|
||||
espiar a operação pode dar acesso ao topo sem modificar o _stack_.
|
||||
nome alternativo, LIFO (last in, first out). Adicionalmente, uma operação
|
||||
de espiada (peek) pode dar acesso ao topo sem modificar o _stack_.
|
||||
O nome "stack" para este tipo de estrutura vem da analogia de
|
||||
um conjunto de itens físicos empilhados uns sobre os outros,
|
||||
o que facilita retirar um item do topo da pilha, enquanto para chegar a
|
||||
|
||||
@ -8,7 +8,7 @@
|
||||
|
||||
Na ciência da computação, uma **árvore** é uma estrutura de dados
|
||||
abstrada (ADT) amplamente utilizada - ou uma estrutura de dados
|
||||
implementando este ADT que simula uma estrutura hierarquica de árvore,
|
||||
implementando este ADT que simula uma estrutura hierárquica de árvore,
|
||||
com valor raíz e sub-árvores de filhos com um nó pai, representado
|
||||
como um conjunto de nós conectados.
|
||||
|
||||
|
||||
@ -1,9 +1,9 @@
|
||||
# Trie
|
||||
# Árvore de Prefixos (Trie)
|
||||
|
||||
Na ciência da computação, uma **trie**, também chamada de árvore digital (digital tree)
|
||||
e algumas vezes de _radix tree_ ou _prefix tree_ (tendo em vista que eles
|
||||
podem ser pesquisados por prefixos), é um tipo de árvore de pesquisa, uma
|
||||
uma estrutura de dados de árvore ordenada que é usado para armazenar um
|
||||
podem ser pesquisados por prefixos), é um tipo de árvore de pesquisa, uma
|
||||
estrutura de dados de árvore ordenada que é usado para armazenar um
|
||||
conjunto dinâmico ou matriz associativa onde as chaves são geralmente _strings_.
|
||||
Ao contrário de uma árvore de pesquisa binária (binary search tree),
|
||||
nenhum nó na árvore armazena a chave associada a esse nó; em vez disso,
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user